KUMPULAN RUMUS MATEMATIKA SMA

RUMUS MATEMATIKA SMA
Oleh Russel Sng

Bab 1

Rumus-Rumus Trigonometri (Matematika)

 

A. Bentuk Umum

B. Sudut-Sudut Istimewa

C. Hubungan Sudut Berelasi antara Sin, Cos dan Tangen



D. Rumus-rumus Trigonometri

1. Aturan sinus


2. Aturan Cosinus


3. Luas Segitiga ABC


4. Jumlah dan Selish Dua Sudut



5. Sudut 2A (Sudut Kembar)


6. Hasil Kali Dua Fungsi Trigonometri


7. Jumlah Selisih Dua Fungsi Trigonometri


8. Persamaan Trigonometri


9. Bentuk a Cos x + b Sin x


10. Bentuk a Cos x + b Sin x = c

11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x 

  Bab 2 

Perhitungan Konversi Satuan

Dalam perhitungan khususnya dalam dunia IPA, kita kembutuhkan keahlian dalam perhitungan. Dan terkadang terdapat perhitungan yang memerlukan konversi.

Angka dan satuan terkait dalam besaran apapun yang kita ukur, seperti panjang, massa atau kecepatan. Sering kita diberikan besaran dalam satuan tertentu dan kita kita ingin menyatakannya dalam satuan lain. Misalnya kita mengetahui jarak dua desa dalam satuan meter dan kita ingin mengetahui berapa jaraknya dalam satuan kilometer. Demikian pula dengan massa benda. Misalnya kita mengukur berat badan kita dalam satuan kg dan kita ingin mengetahui berat badan kita dalam satuan pon. Untuk itu kita harus mengkonversi satuan tersebut. Konversi berarti mengubah. Untuk mengkonversi satuan, terlebih dahulu harus diketahui beberapa hal yang penting, antara lain awalan-awalan metrik yang digunakan dalam satuan dan faktor konversi.

Awalan-awalan satuan yang sering digunakan dapat anda lihat pada tabel berikut ini.

km = kilometer

hm = hektometer

dam = dekameter

m = meter

dm = desimeter

cm = centimeter

mm = milimeter

Konversi Satuan SI
Kelebihan sistem Satuan Internasional (SI) adalah kemudahan dalam pemakaiannya karena menggunakan sistem desimal (kelipatan 10) dan hanya ada satu satuan pokok untuk setiap besaran dengan penambahan awalan untuk satuan yang lebih besar atau lebih kecil. Misalnya, 1 centimeter = 0,01 meter atau 1 kilogram sama dengan 1000 gram. Untuk kemudahan mengubah suatu satuan ke satuan lain dapat dilakukan dengan menggunakan bantuan tangga konversi seperti yang terlihat pada gambar di bawah ini.

kg = kilogram

hg = hektogram

dag = dekagram

g = gram

dg = desigram

cg = centigram

mg = miligram

Cara mengkonversi satuan-satuan SI dengan tangga konversi :

Pertama, Letakkan satuan asal yang akan dikonversi dan satuan baru yang akan dicari pada tangga sesuai dengan urutan tangga konversi

Kedua, Hitung jumlah langka yang harus ditempuh dari satuan asal ke satuan baru

a. Jika satuan baru berada di bawah satuan asal ( menuruni tangga ), maka :
* Setiap turun satu tangga, bilangan asal dikali 10
* Setiap turun dua tangga, bilangan asal dikali 10
* Setiap turun tiga tangga, bilangan asal dikali 1000, dan seterusnya

b. Jika satuan baru berada di atas satuan asal ( menaiki tangga ), maka :
* Setiap naik satu tangga, bilangan asal dibagi 10
* Setiap naik dua tangga, bilangan asal dibagi 100
* Setiap naik tiga tangga, bilangan asal dibagi 1000, dan seterusnya

Contoh soal :

Ubahlah satuan berikut ini ?

10 km = …. cm ?

Perhatikan Tangga Konversi Satuan Panjang.

Dari km (kilometer) ke cm (centimeter), kita menuruni 5 anak tangga. Dengan demikian kita mengalikannya dengan 100.000 (5 nol). Jadi 10 km = 10 x 100000 = 1000.000 cm

7000 m = ….. km ?

Perhatikan Tangga Konversi Satuan Panjang.

Dari m (meter) ke km (kilometer), kita menaiki 3 anak tangga. Dengan demikian kita membaginya dengan 1000 (3 nol). Jadi 7000 km = 7000 : 1000 = 7 km

300 gr = ….. kg ?

Perhatikan Tangga Konversi Satuan massa.

Dari gr (gram) ke kg (kilogram), kita menaiki 3 anak tangga. Dengan demikian kita membaginya dengan 1000 (3 nol). Jadi 300 gr = 300 : 1000 = 0,3 kg

5 kg = …. mg ?

Perhatikan Tangga Konversi Satuan massa.

Dari kg (kilogram) ke mg (miligram), kita menuruni 6 anak tangga. Dengan demikian kita mengalikannya dengan 1.000.000 (6 nol). Jadi 5 kg = 5 x 1000.000 = 5.000.000 kg


FAKTOR KONVERSI
Selain mengkonversi satuan dalam sistem internasional, kita juga harus mengetahui konversi satuan dalam sistem yang berbeda, antara lain dari satuan Sistem Internasional ke Sistem British atau sebaliknya. Sebagai contoh, kita mengukur panjang sebuah meja dalam satuan inchi dan kita ingin menyatakannya dalam centimeter. Untuk itu kita perlu mengetahui faktor konversi. Faktor konversi dapat anda lihat pada tabel di bawah ini.

Contoh Soal :

Ubahlah satuan panjang berikut ini :

15 inchi = ….. m ?

Perhatikan Faktor Konversi Panjang.

1 inchi = 2,54 cm. —– 1 cm = 0,01 m (lihat tangga konversi panjang)

Jadi, 15 inchi = 15 x 2,54 cm = 38,1 cm —— 38,1 cm = 38,1 x 0,01 m = 0,381 meter.

100 mil = …. cm ?

Perhatikan Faktor Konversi Panjang.

1 mil = 1,61 km. —– 1 km = 100.000 cm (lihat tangga konversi panjang)

Jadi, 100 mil = 100 x 1,61 km = 161 km —- 161 km = 161 x 100.000 cm

= 16.100.000 cm.

100 km = …. mil ?

Perhatikan Faktor Konversi Panjang.

1 km = 0,621 mil.

Jadi, 100 km = 100 x 0,621 mil = 62,1 mil.

Ubahlah satuan Kelajuan berikut ini :

(Catatan : Knot merupakan satuan kelajuan yang biasa digunakan Kapal Laut)
50 Knot = …. km/jam ?

Perhatikan Faktor Konversi Panjang.

1 knot = 1,151 mil/jam —– 1 mil/jam = …. Km/jam ?

1 mil = 1,61 km (lihat Faktor Konversi Panjang)

Jadi, 1 mil/jam = 1,61 km/jam

50 Knot = 50 x 1,61 km/jam = 80,5 km/jam

 

Bab 3

Sekilas Tentang Logaritma Matematika

Mari belajar sekilas tentang logaritma..
Jika n adalah logaritma dari a dengan bilangan pokok p, maka berlaku :

^plog a = n <---> pⁿ = a

Dengan catatan : a>0, p>0, dan p≠1

Setelah itu, barulah kita mempelajari sifat-sifat logaritma yang bisa kita terapkan di berbagai persoalan.

Sifat-sifat logaritma :
1. ^plog ( ab ) = ^plog a + ^plog b
2. ^alog aⁿ = n
3. ^plog (a/b) = ^plog a - ^plog b
4. ^plog 1 = 0
5. ^plog aⁿ = n . ^alog a
6. ^plog a . ^alog q = ^plog q
7. ^pnlog a^m = m/n ^plog a
8. ^plog p = 1
9. P^{plog a} = a

1. Bila bilangan pokok suatu logaritma tidak diberikan, maka maksudnya logaritma tersebut berbilangan pokok = 10.
   [log 7 maksudnya ¹⁰log 7 ]

1. logⁿx adalah cara penulisan untuk (logx)ⁿBedakan dengan log xⁿ = n log x

Contoh soal :
Jika ³log 4 = p dan ²log 5 = q maka nilai untuk ³log 5 ?

2log 5 = 22log 52 = 2 . 4log 5 = 4log 5 =

q q q 1/2 q

³log 4 . ⁴log 5 = ³log 5
maka ³log 5 = 1/2 (pq)

Bab 4

Barisan dan Deret Aritmetika

 

Pada pembelajaran matematika di kelas XII SMA ada sebuah BAB yang mempelajari tentang BARISAN dan DERET. Semoga postingan ini dapat membantu bagi teman-teman yang kesulitan memahami materinya.

BARISAN ARITMATIKA

U₁, U₂, U₃, .......U_n-1, U_n disebut barisan aritmatika, jika
U₂ - U₁ = U₃ - U₂ = .... = U_n - U_n-1 = konstanta

Selisih ini disebut juga beda (b) = b =U_n - U_n-1 

Suku ke-n barisan aritmatika a, a+b, a+2b, ......... , a+(n-1)b
                                      U₁, U₂,   U₃ ............., U_n

Rumus Suku ke-n :

U_n = a + (n-1)b = bn + (a-b) ® Fungsi linier dalam n

• DERET ARITMATIKA

a + (a+b) + (a+2b) + . . . . . . + (a + (n-1) b) disebut deret aritmatika.a = suku awal
b = beda
n = banyak suku
U_n = a + (n - 1) b adalah suku ke-nJumlah n suku

Sn = 1/2 n(a+U_n)
      = 1/2 n[2a+(n-1)b]
      = 1/2bn² + (a - 1/2b)n ® Fungsi kuadrat (dalam n)
Keterangan:

1. Beda antara dua suku yang berurutan adalah tetap (b = S_n")

1. Barisan aritmatika akan naik jika b > 0
   Barisan aritmatika akan turun jika b < 0

1. Berlaku hubungan U_n = S_n - S_n-1 atau Un = S_n' - 1/2 S_n"

1. Jika banyaknya suku ganjil, maka suku tengah
   
   U_t = 1/2 (U₁ + U_n) = 1/2 (U₂ + U_n-1)          dst.

1. S_n = 1/2 n(a+ U_n) = nU_t ® U_t = Sn / n

1. Jika tiga bilangan membentuk suatu barisan aritmatika, maka untuk memudahkan perhitungan misalkan bilangan-bilangan itu adalah a - b , a , a + b

  Bab 5

Penjelasan mengenai Barisan dan Deret Geometri

Pada postingan sebelumnya terdapat pembahasan mengenai barisan dan deret aritmatika, nah kali ini postingnya membahas tentang bagian lain dari BAB Barisan dan Deret pada pembelajaran Matematika di kelas XII, semoga posting ini dapat membantu bagi teman-teman yang kesulitan dalam pembelajaran ini..

BARISAN GEOMETRI 

Barisan yang suku-sukunya diperoleh dengan mengalikan suatu bilangan tetap ke suku sebelumnya. Bilangan tetap itu disebut rasio (pembanding) dilambangkan dengan r. Jika suku pertama (U₁) dinotasikan a dan rasio dinyatakan dengan r, maka suku-suku barisan geometri dapat dituliskan sebagai berikut: a, ar, ar², ……, ar^n-1.

Sehingga suku ke-n suatu barisan geometri dirumuskan : U_n= ar^n-1
Sedangkan jika Un dibagi dengan Un-1 didapat r,
sehingga  diperoleh rumus untuk r :

DERET GEOMETRI

Jika pada barisan geometri tanda “,” diganti dengan tanda “+” maka didapat deret geometri.

Bentuk baku deret geometri adalah:  a + ar + ar² + …… + ar^n-1 . Jumlah n  suku pertama deret geometri dinyatakan dengan S_n, dan dirumuskan:

Untuk deret geometri dengan -1< r <1 dikatakan bahwa deret tersebut konvergen atau mempunyai jumlah sampai tak hingga suku.

Jumlah takhingga dilambangkan dengan S ~ dan dirumuskan :

 

DERET GEOMETRI TAK BERHINGGADeret Geometri tak berhingga adalah penjumlahan dari

U₁ + U₂ + U₃ + ..............................
¥
å Un = a + ar + ar² .........................
n=1 
dimana n ® ¥ dan -1 < r < 1 sehingga rⁿ ® 0
Dengan menggunakan rumus jumlah deret geometri didapat :Jumlah tak berhingga    S_¥ = a/(1-r)Deret geometri tak berhingga akan konvergen (mempunyai jumlah) untuk -1 < r < 1

Catatan:

a + ar + ar² + ar³ + ar⁴ + .................Jumlah suku-suku pada kedudukan ganjil
a+ar² +ar⁴+ .......                     S_ganjil = a / (1-r²)Jumlah suku-suku pada kedudukan genap
a + ar³ + ar⁵ + ......                  S_genap = ar / 1 -r² 
Didapat hubungan : S_genap / S_ganjil = r

PENGGUNAAN

Perhitungan BUNGA TUNGGAL (Bunga dihitung berdasarkan modal awal)

M₀, M₁, M₂, ............., M_n

M₁ = M₀ + P/100 (1) M₀ = {1+P/100(1)}M₀

M₂ = M₀ + P/100 (2) M₀ = {1+P/100(2)} M₀

.
.
.
.

M_n =M₀ + P/100 (n) M₀ ® M^_n = {1 + P/100 (n) } M₀

Perhitungan BUNGA MAJEMUK (Bunga dihitung berdasarkan modal terakhir)

M₀, M₁, M₂, .........., M_n

M₁ = M₀ + P/100 . M₀ = (1 + P/100) M₀

M₂ = (1+P/100) M₀ + P/100 (1 + P/100) M₀ = (1 + P/100)(1+P/100)M₀      = (1 + P/100)² M₀.
.
.

Mn = {1 + P/100}ⁿ M₀

Keterangan :

M₀ = Modal awalM_n = Modal setelah n periodep   = Persen per periode atau suku bungan   = Banyaknya periode

Catatan:

Rumus bunga majemuk dapat juga dipakai untuk masalah pertumbuhan tanaman, perkembangan bakteri (p > 0) dan juga untuk masalah penyusutan mesin, peluruhan bahan radio aktif (p < 0).

LATIHAN SOAL

 1.   Tentukan suku yang diminta dari barisan :

      a) 1,3,9,..... suku ke-7

      b) 3,6,12,....suku ke-8

      c) 16,8,4, ... suku ke-10

2.  Tentukan rasio dan suku ke-5 dari barisan geometri jika diketahui sebagai berikut:

1. U₁ = 2,  U₃ = 8

1. U₁ = 4U_3, U₄ = ¼

1. U₁ = 36, U₂ = –12

1. U₁.U₅ = 16, U₂ + U₄ = 10

1. U₁ + U₆ = 244, U₃.U₄ = 243

 3. Carilah nilai x jika barisan berikut adalah barisan geometri.

1. x + 1, x – 1, dan x – 5

1. 2x, x² dan 8x

1. 4 + x, 3 + 3x dan 1 + 7x

1. x – 1, 2x – 8 dan 5 – x

1. 2x – 5, x – 4 dan 10 – 3x

4.  Diketahui barisan geometri : 1, 9, 81, ……. Diantara tiap dua suku berurutan disisipkan sebuah suku sehingga terbentuk barisan geometri baru.  Tentukan rasio dan suku ke-7 barisan geometri baru.

5. Suatu modal sebesar M rupiah ditabung di Bank dan mendapatkan bunga majemuk p% setiap tahun.  Tentukan modal setelah n tahun.

6. Sebuah mobil harganya Rp. 300.000.000,- setiap tahun harga mobil itu menyusut 10% dari harga tahun sebelumnya.

1. hitunglah harga mobil pada akhir tahun ke-1, 2, 3, dan 4.

1. Jika setelah n tahun harga mobil itu adalah Tn, tunjukkan bahwa Tn = Rp. 300.000.000,- x (0,9)ⁿ

7.  Pada sebuah deret geometri dibutuhkan U₁ + U₂ = 4, U_n–1 + U_n = 108 dan S_n = 121.  tentukan a dan r

8.  Diketahui bahwa jumlah n suku suatu deret adalah S_n = 3(2ⁿ – 1) 

1. Buktikan bahwa deret itu adalah deret geometri

1. Tentukan suku pertama, rasio dan suku ke-10

1. Carilah n terkecil agar jumlah n suku pertamanya lebih besar dari 104

9.  Uang sebesar Rp. 2.000.000,- diinvestasikan pada tiap awal tahun dengan mendapat bunga majemuk 12%  

    pertahun.  Hitunglah seluruh uang tersebut pada akhir tahun ketujuh. 

10.   x₁ dan x₂ adalah akar-akar bulat dari persamaan x² – (2k + 4)x + (3k + 4) = 0.  Jika x₁, k dan x₂ merupakan tiga suku pertama barisan geometri.  Tentukan jumlah ketiga bilangan tersebut.

11.  Diantara setiap dua suku berurutan pada deret geometri 7 + 28 + 112 + …… sampai 6 suku disisipkan sebuah suku sehingga diperoleh deret geometri baru.  Hitunglah jumlah suku-suku yang disisipkan.

  Bab 6

Penjelasan Rumus Phytagoras

Tahu kan rumus yang satu ini, itu loh, rumus untuk mencari nilai dari panjang sisi sebuah segitiga. Bagi yang belum mengerti berikut penjelasannya.

Rumus asli phytagoras 

Dari gambar diatas, kita buktikan kebenarannya, di mulai dengan membuat gambar sebuah persegi besar, kemudian gambarlah sebuah persegi kecil di dalam persegi besar tersebut, seperti gambar berikut:

Perhitungan Phytagoras  :
Luas persegi besar = Luas persegi kecil + 4 Luas segitiga
( b + a ) . ( b + a ) = c . c + 4 . 1/2 b.a 

b² + 2 b.a + a² = c² + 2 b.a

b ² + a² = c² + 2 b.a - 2 b.a

b ² + a² = c²

Berdasarkan Rumus Phytagoras  tersebut terbukti bahwa sisi miring sebuah segitiga siku - siku adalah akar dari jumlah kuadrat sisi - sisi yang lain.

Berikut cara penggunaannya.:

Apabila kita mencari Sisi Miring ( C ) Rumus = a² + b² = n,, n= akar n = hasil nya
Tidak Susah Kan??? 

Kalau Kalian Ingin Mencari sisi Alas( A ) Rumus = b² - c²=n,, n= akar n = hasil nya(apabila B panjang nya lebih panjang berarti di kurangi c.nah C Lebih Besar Juga sebaliknya) 

kalau mencari tinggi (b) Sama seperti mencari Alas.Tetapi kalau Ini B nnya Di ganti Dengan A.

Mari Kita Pakai Soal Agar Lebih Mengerti

Soal : 

Sisi A= 20 cm Sisi b= 15 cm Sisi c=n?
berapakah Sisi C.
Cara Mencari nya seperti Di atas.masih Inget kan?
Jawab :
:: 20² + 15² = 400 + 225 = 625 .. Akar Dari 625= 25 Jadi Sisi c Samadengan = 25

Soal :
Kalau Sisi B= 25 cm Sisi C= 15 cm A= N??
Jawab :
:: 25² - 15² = 625 - 225 = 400 .. akar dari 400 = 20 cm Jadi sisi B 20 cm(apabila Mencari Yang sisi A sama seperti B)

Mudah bukan, selamat mencoba..

Bab 7

Rumus Luas dan Volume Bangun Kerucut

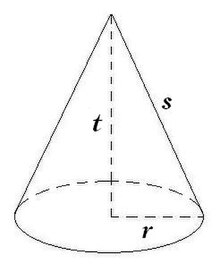
Dalam matematika, kita akan mempelajari tentang bangun ruang. Kali ini kami akan membahas tentang rumus bangun kerucut. 

Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.

Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang lengkung yang disebut selimut kerucut.

Unsur-unsur Kerucut:
Kerucut memiliki 1 titik sudut, 1 rusuk dan 2 sisi .

Luas dan volume kerucut
• Luas permukaan kerucut atau luas kerucut :
L = luas sisi alas + luas selimut kerucut
   = π r² + π r s

   = π r (r + s)

•Volume kerucut :
V = 1/3 x luas alas x tinggi

   = 1/3 x π r² x t

   = 1/3 π r²t

  Bab 8

Rumus Matematika Peluang

Di pembelajaran Matematika kelas XII kita akan mempelajari bab yang berisikan materi peluang, semoga posting ini dapat bermanfaat bagi teman-teman pelajar.

Peluang Matematika

 1. Pengertian Ruang Sampel dan Kejadian 
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S. 

Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}

2. Pengertian Peluang Suatu Kejadian 
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :  

Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3

3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan  
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti. 

4. Frekuensi Harapan Suatu Kejadian 
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ). 

Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga : 

Frekuensi harapan munculnya mata dadu 1 adalah

5. Peluang Komplemen Suatu Kejadian 
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga : 
 
Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P). 

Peluang Kejadian Majemuk

1. Gabungan Dua Kejadian 
Untuk setiap kejadian A dan B berlaku :  

Catatan : dibaca “ Kejadian A atau B dan  dibaca “Kejadian A dan B” 

Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :

2. Kejadian-kejadian Saling Lepas 
Untuk setiap kejadian berlaku  Jika  . Sehingga Dalam kasus ini, A dan B disebut dua kejadian saling lepas. 

3. Kejadian Bersyarat 
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika  adalah peluang terjadinya A dan B, maka  Dalam kasus ini, dua kejadian tersebut tidak saling bebas. 

4. Teorema Bayes 
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :  

5. Kejadian saling bebas Stokhastik 
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga: 
 

Sebaran Peluang

1. Pengertian Peubah acak dan Sebaran Peluang. 
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap dan setiap  maka: 
 

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut : 
 

2. Sebaran Binom 
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut : 

 
Dengan P sebagai parameter dan  
Rumus ini dinyatakan sebagai: 
 untuk n = 0, 1, 2, .... ,n 
Dengan P sebagai parameter dan  

P = Peluang sukses 
n = Banyak percobaan 
x = Muncul sukses 
n-x = Muncul gagal

 

Bab 9

Rumus Matematika Untuk Mean, Median dan

Modus dan contoh soalnya.

Di pembelajaran MATEMATIKA kelas XI, kita akan mempelajari bab statistik, di posting kali ini, akan dijelaskan mengenai Rumus Matematika untuk MEAN, MODUS, MEDIAN dan beberapan bagian yang lainnya. Penjellasannya sebagai berikut:

1. Rumus Rataan Hitung (Mean) 
Rata-rata hitung atau mean memiliki perhitungan dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung disebut dengan mean.

a) Rumus Mean dari Data Tunggal  

b) Rumus Mean Untuk Data yang Disajikan Dalam Distribusi Frekuensi.

Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i

c) Rumus Mean Gabungan

2. Rumus Modus 

a. Data yang belum dikelompokkan

Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan

Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:

Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya

3. Rumus Median (Nilai Tengah) 

a) Data yang belum dikelompokkan
Untuk mencari nilai median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar. 

b) Rumus Data yang Dikelompokkan

Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data

4. Rumus Jangkauan ( J )
Rumus jangkauan yaitu selisih antara nilai data terbesar dengan nilai data terkecil. 

 

5. Rumus Simpangan Quartil (Qd)

Rumus simpangan quartil yaitu:

6. Rumus Simpangan baku ( S ) 

Menentukan rumus simpangan baku yaitu dengan cara:

7. Rumus Simpangan rata – rata (SR) 

8. Rumus Ragam (R)

Contoh soal statistika
Tabel 1.1 dibawah ini:

Jawab :

Contoh soal sederhana:
Berikut ini terdapat data nilai matematika siswa kls VII.A,
andi 85
audi 90
dessy 75
fany 68
hariz 70
joko 80
sinta 75
umaima 74
zeckry 82
Tentukan nilai mean, median, dan modus dari data tersebut.?

Penyelesaian:
urutkan data-data tersebut terlebih dahulu berdasarkan nilai dari terendah hingga teritnggi,
68
70
74
75
75
80
82
85
90
diketahui jmlh anak (n)= 9 org, maka
jumlah nilai= 68+70+74+75+75+80+82+85+90= 699

Mean= 699/9 = 77,667
Jadi, nilai rata-rata siswa kls VII.A untuk pelajaran matematika = 77,667

Median= nilai tengah dari kelompok data tersebut adalah nilai 75

Modus= terdapat 2 nilai 75 dalam kelompok data, sehingga modus= 75

Cukup mudah bukan materi tentang mean, median dan modus, bagaimaba pendapat kamu?
Jangan lupa untuk membaca materi matematika lainnya. 

  Bab 10

Operasi Penjumlahan dan Perasionalan Pada Pecahan

Masih ingat bentuk berikut :
3² = 3 x 3
2³ = 2 x 2 x 2
5⁶ = 5 x 5 x 5 x 5 x 5 x 5
Demikian seterusnya sehingga diperoleh bentuk umum sebagai berikut.

Dengan a bilangan bulat dan n bilangan bulat positif Dari pengertian di atas akan diperoleh sifat-sifat berikut.

Sifat 1
aⁿ x aⁿ = a^{m + n}
2⁴ x 2³ = (2 x 2 x 2 x 2 )x(2 x 2 x 2 )
           = 2 x 2 x 2 x 2 x 2 x 2 x 2
           = 27
           = 2⁴⁺³

Sifat 2
a^m : aⁿ = a^{m - n}, m > n
5⁵ : 5³ = (5 x 5 x 5 x 5 x 5) : (5 x 5 x 5)
           = 5 x 5
           = 52
           = 5^{5 - 3}

Sifat 3
(a^m)ⁿ = a^{m x n}
(3⁴)² = 3⁴ x 3⁴
       = (3 x 3 x 3 x 3) x (3 x 3 x 3 x 3)
       = (3 x 3 x 3 x 3 x 3 x 3 x 3 x 3)
       = 38
       = 3^{4 x 2}

Sifat 4
(a x b)^m = a^m x b^m
(4 x 2)³ = (4 x 2) x (4 x 2) x (4 x 2)
           = (4 x 4 x 4) x (2 x 2 x 2)
           = 4³ x 2³

Sifat 5
(a : b)^m = a^m : b^m
(6 : 3) ⁴ = (6 : 3) x (6 : 3) x (6 : 3) x (6 : 3)
            = (6 x 6 x 6 x 6) : (3 x 3 x 3 x 3)
            = 6⁴ : 3⁴

Bilangan Bulat dengan Eksponen Bilangan Bulat Negatif

Dari pola bilangan itu dapat disimpulkan bahwa 2⁰ = 1 dan 2^-n = ¹/_2ⁿ , secara umum dapat ditulis :

Pecahan Berpangkat Bilangan Bulat
Kita telah mengetahui bahwa pecahan adalah bilangan dalam bentuk dengun a dan b bilangan bulat (b ≠ 0). Bagaimanakah jika pecahan dipangkatkan dengan bilangan bulat? Untuk menentukan hasil pecahan yang dipangkatkan dengan bilangan bulat, caranya sama dengan menentukan hasil bilangan bulat yang dipangkatkan dengan bilangan bulat.

Contoh:
Tentukan hasil berikut ini!

 (¹/₂)⁵
Jawab :

Bentuk Akar dan Bilangan Berpangkat Pecahan

Bilangan Rasional dan Irasional

Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional merupakan gabungan dari bilangan bulat, nol, dan pecahan. Contoh bilangan rasional adalah -5, ^-1/₂, 0, 3, ³/₄, dan ⁵/_9.

Sebaliknya, bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0.
Contoh bilangan irasional adalah . Bilangan-bilangan tersebut, jika dihitung dengan kalkulator merupakan desimal yang tak berhenti atau bukan desimal yang berulang. Misalnya 

√2 = 1,414213562 .... Selanjutnya, gabungan anrara bilangan rasional dan irasional disebut bilangan real.

Bentuk Akar

Berdasarkan pembahasan sebelumnya, contoh bilangan irasional adalah √2 dan √5 . Bentuk seperti itu disebut bentuk akar. Dapatkah kalian menyebutkan contoh yang lain?

Bentuk akar adalah akar dari suatu bilangan yang hasilnya bukan bilangan Rasional.

Bentuk akar dapat disederhanakan menjadi perkalian dua buah akar pangkat bilangan dengan salah satu akar memenuhi definisi
√a² = a jika a ≥ 0, dan –a jika a < 0

Contoh :
Sederhanakan bentuk akar berikut √75
Jawab :
√75 = √25x3 = √25 x √3 = 5√3

Mengubah Bentuk Akar Menjadi Bilangan Berpangkat Pecahan dan Sebaliknya

Bentuk √a dengan a bilangan bulat tidak negatif disebut bentuk akar kuadrat dengan syarat tidak ada bilangan yang hasil kuadratnya sama dengan a. oleh karena itu √2,√3, √5, √10, √15 dan √19 merupakan bentuk akar kuadrat. Untuk selanjutnya, bentuk akar ⁿ√a^m dapat ditulis a^m/n(dibaca: a pangkat m per n). Bentuk a^m/n disebut bentuk pangkat pecahan.

contoh :
 

jawab :

Operasi Aljabar pada Bentuk Akar

Penjumlahan dan Pengurangan

Penjumlahan dan pengurangan pada bentuk akar dapat dilakukan jika memiliki suku-suku yang sejenis.

kesimpulan :
jika a, c = Rasional dan b ≥ 0, maka berlaku 

a√b + c√b = (a + c)√b

a√b - c√b = (a - c)√b

Perkalian dan Pembagian

Contoh :
Tentukan hasil operasi berikut :

jawab :

Perpangkatan

Kalian tentu masih ingat bahwa (a^)" = a^'. Rumus tersebut juga berlaku pada operasi perpangkatan dari akar suatu bilangan.
Contoh:

Operasi Campuran

Dengan memanfaatkan sifat-sifat pada bilangan berpangkat, kalian akan lebih mudah menyelesaikan soal-soal operasi campuran pada bentuk akarnya. Sebelum melakukan operasi campuran, pahami urutan operasi hitung berikut.

• Prioritas yang didahulukan pada operasi bilangan adalah bilangan-bilangan yang ada dalam tanda kurung.

• Jika tidak ada tanda kurungnya maka

1. pangkat dan akar sama kuat;

1. kali dan bagi sama kuat;

1. tambah dan kurang sama kuat, artinya mana yang lebih awal dikerjakan terlebih dahulu;

1. kali dan bagi lebih kuat daripada tambah dan kurang, artinya kali dan bagi dikerjakan terlebih dahulu.

Contoh :

Merasionalkan Penyebut

Dalam perhitungan matematika, sering kita temukan pecahan dengan penyebut bentuk akar, misalnya 

Agar nilai pecahan tersebut lebih sederhana maka penyebutnya harus dirasionalkan terlebih dahulu. Artinya tidak ada bentuk akar pada penyebut suatu pecahan. Penyebut dari pecahan-pecahan yang akan dirasionalkan berturut-turut adalah 

Merasionalkan penyebut adalah mengubah pecahan dengan penyebut bilangan irasional menjadi pecahan dengan penyebut bilangan rasional.

Penyebut Berbentuk √b

Jika a dan b adalah bilangan rasional, serta √b adalah bentuk akar maka pecahan ^a/_√b dapat dirasionalkan penyebutnya dengan cara mengalikan pecahan tersebut dengan ^√b/_√b .
 

Contoh :
Sederhanakan pecahan berikut dengan merasionalkan penyebutnya!

jawab :

Penyebut Berbentuk (a+√b) atau (a+√b)

Jika pecahan-pecahan mempunyai penyebut berbentuk (a+√b) atau (a+√b) maka pecahan tersebut dapat dirasionalkan dengan cara mengalikan pembilang dan penyebutnya dengan sekawannya. Sekawan dari (a+√b) adalah (a+√b) adalah dan sebaliknya.
Bukti

Contoh :

Rasionalkan penyebut pecahan berikut.

jawab :

 

Penyebut Berbentuk (√b+√d) atau (√b+√d)

Pecahan tersebut dapat dirasionalkan dengan mengalikan pembilang dan penyebutnya dengan bentuk akar sekawannya, yaitu sebagai berikut.

Contoh:

Selesaikan soal berikut!

Jawab :

Referensi

• Tiga Serangkai

• http://bebas.vlsm.orgMasih ingat bentuk berikut :
  
  3² = 3 x 3
  2³ = 2 x 2 x 2
  5⁶ = 5 x 5 x 5 x 5 x 5 x 5
  Demikian seterusnya sehingga diperoleh bentuk umum sebagai berikut.
  
  
  
  
  
  Dengan a bilangan bulat dan n bilangan bulat positif Dari pengertian di atas akan diperoleh sifat-sifat berikut.
  
  
  Sifat 1
  aⁿ x aⁿ = a^{m + n}
  2⁴ x 2³ = (2 x 2 x 2 x 2 )x(2 x 2 x 2 )
             = 2 x 2 x 2 x 2 x 2 x 2 x 2
             = 27
             = 2⁴⁺³
  
  
  Sifat 2
  a^m : aⁿ = a^{m - n}, m > n
  5⁵ : 5³ = (5 x 5 x 5 x 5 x 5) : (5 x 5 x 5)
             = 5 x 5
             = 52
             = 5^{5 - 3}
  
  
  Sifat 3
  (a^m)ⁿ = a^{m x n}
  (3⁴)² = 3⁴ x 3⁴
         = (3 x 3 x 3 x 3) x (3 x 3 x 3 x 3)
         = (3 x 3 x 3 x 3 x 3 x 3 x 3 x 3)
         = 38
         = 3^{4 x 2}
  
  
  Sifat 4
  (a x b)^m = a^m x b^m
  (4 x 2)³ = (4 x 2) x (4 x 2) x (4 x 2)
             = (4 x 4 x 4) x (2 x 2 x 2)
             = 4³ x 2³
  
  
  Sifat 5
  (a : b)^m = a^m : b^m
  (6 : 3) ⁴ = (6 : 3) x (6 : 3) x (6 : 3) x (6 : 3)
              = (6 x 6 x 6 x 6) : (3 x 3 x 3 x 3)
              = 6⁴ : 3⁴
  
  
  Bilangan Bulat dengan Eksponen Bilangan Bulat Negatif
  
  
  
  
  
  Dari pola bilangan itu dapat disimpulkan bahwa 2⁰ = 1 dan 2^-n = ¹/_2ⁿ , secara umum dapat ditulis :
  
  
  
  
  
  Pecahan Berpangkat Bilangan Bulat
  Kita telah mengetahui bahwa pecahan adalah bilangan dalam bentuk dengun a dan b bilangan bulat (b ≠ 0). Bagaimanakah jika pecahan dipangkatkan dengan bilangan bulat? Untuk menentukan hasil pecahan yang dipangkatkan dengan bilangan bulat, caranya sama dengan menentukan hasil bilangan bulat yang dipangkatkan dengan bilangan bulat.
  
  
  Contoh:
  Tentukan hasil berikut ini!
  
  
   (¹/₂)⁵
  Jawab :
  
  
  
  Bentuk Akar dan Bilangan Berpangkat Pecahan
  
  
  Bilangan Rasional dan Irasional
  
  
  Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional merupakan gabungan dari bilangan bulat, nol, dan pecahan. Contoh bilangan rasional adalah -5, ^-1/₂, 0, 3, ³/₄, dan ⁵/_9.
  
  
  Sebaliknya, bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0.
  Contoh bilangan irasional adalah . Bilangan-bilangan tersebut, jika dihitung dengan kalkulator merupakan desimal yang tak berhenti atau bukan desimal yang berulang. Misalnya 
  
  
  √2 = 1,414213562 .... Selanjutnya, gabungan anrara bilangan rasional dan irasional disebut bilangan real.
  
  
  Bentuk Akar
  
  
  Berdasarkan pembahasan sebelumnya, contoh bilangan irasional adalah √2 dan √5 . Bentuk seperti itu disebut bentuk akar. Dapatkah kalian menyebutkan contoh yang lain?
  
  
  Bentuk akar adalah akar dari suatu bilangan yang hasilnya bukan bilangan Rasional.
  
  
  Bentuk akar dapat disederhanakan menjadi perkalian dua buah akar pangkat bilangan dengan salah satu akar memenuhi definisi
  √a² = a jika a ≥ 0, dan –a jika a < 0
  
  
  Contoh :
  Sederhanakan bentuk akar berikut √75
  Jawab :
  √75 = √25x3 = √25 x √3 = 5√3
  
  
  Mengubah Bentuk Akar Menjadi Bilangan Berpangkat Pecahan dan Sebaliknya
  
  
  Bentuk √a dengan a bilangan bulat tidak negatif disebut bentuk akar kuadrat dengan syarat tidak ada bilangan yang hasil kuadratnya sama dengan a. oleh karena itu √2,√3, √5, √10, √15 dan √19 merupakan bentuk akar kuadrat. Untuk selanjutnya, bentuk akar ⁿ√a^m dapat ditulis a^m/n(dibaca: a pangkat m per n). Bentuk a^m/n disebut bentuk pangkat pecahan.
  
  
  contoh :
   
  
  
  jawab :
  
  
  
  
  
  Operasi Aljabar pada Bentuk Akar
  
  
  Penjumlahan dan Pengurangan
  
  
  Penjumlahan dan pengurangan pada bentuk akar dapat dilakukan jika memiliki suku-suku yang sejenis.
  
  
  
  
  kesimpulan :
  jika a, c = Rasional dan b ≥ 0, maka berlaku 
  
  
  a√b + c√b = (a + c)√b
  
  
  a√b - c√b = (a - c)√b
  
  
  Perkalian dan Pembagian
  
  
  Contoh :
  Tentukan hasil operasi berikut :
  
  
  
  
  
  jawab :
  
  
  
  
  
  Perpangkatan
  
  
  Kalian tentu masih ingat bahwa (a^)" = a^'. Rumus tersebut juga berlaku pada operasi perpangkatan dari akar suatu bilangan.
  Contoh:
  
  
  
  Operasi Campuran
  
  
  Dengan memanfaatkan sifat-sifat pada bilangan berpangkat, kalian akan lebih mudah menyelesaikan soal-soal operasi campuran pada bentuk akarnya. Sebelum melakukan operasi campuran, pahami urutan operasi hitung berikut.
  
  
  • Prioritas yang didahulukan pada operasi bilangan adalah bilangan-bilangan yang ada dalam tanda kurung.
  • Jika tidak ada tanda kurungnya maka
  
  
  1. pangkat dan akar sama kuat;
  1. kali dan bagi sama kuat;
  1. tambah dan kurang sama kuat, artinya mana yang lebih awal dikerjakan terlebih dahulu;
  1. kali dan bagi lebih kuat daripada tambah dan kurang, artinya kali dan bagi dikerjakan terlebih dahulu.
  
  
  Contoh :
  
  
  
  
  
  Merasionalkan Penyebut
  
  
  Dalam perhitungan matematika, sering kita temukan pecahan dengan penyebut bentuk akar, misalnya 
  
  
  Agar nilai pecahan tersebut lebih sederhana maka penyebutnya harus dirasionalkan terlebih dahulu. Artinya tidak ada bentuk akar pada penyebut suatu pecahan. Penyebut dari pecahan-pecahan yang akan dirasionalkan berturut-turut adalah 
  
  
  Merasionalkan penyebut adalah mengubah pecahan dengan penyebut bilangan irasional menjadi pecahan dengan penyebut bilangan rasional.
  
  
  Penyebut Berbentuk √b
  
  
  Jika a dan b adalah bilangan rasional, serta √b adalah bentuk akar maka pecahan ^a/_√b dapat dirasionalkan penyebutnya dengan cara mengalikan pecahan tersebut dengan ^√b/_√b .
   
  
  
  Contoh :
  Sederhanakan pecahan berikut dengan merasionalkan penyebutnya!
  
  
  
  
  
  jawab :
  
  
  
  
  
  Penyebut Berbentuk (a+√b) atau (a+√b)
  
  
  Jika pecahan-pecahan mempunyai penyebut berbentuk (a+√b) atau (a+√b) maka pecahan tersebut dapat dirasionalkan dengan cara mengalikan pembilang dan penyebutnya dengan sekawannya. Sekawan dari (a+√b) adalah (a+√b) adalah dan sebaliknya.
  Bukti
  
  
  
  Contoh :
  
  
  Rasionalkan penyebut pecahan berikut.
  
  
  
  
  
  jawab :
  
  
   
  
  
  Penyebut Berbentuk (√b+√d) atau (√b+√d)
  
  
  Pecahan tersebut dapat dirasionalkan dengan mengalikan pembilang dan penyebutnya dengan bentuk akar sekawannya, yaitu sebagai berikut.
  
  
  
  Contoh:
  
  
  Selesaikan soal berikut!
  
  
  
  
  
  Jawab :
  
  
  
  
  
  
  
  
  
  Bab 11
  Permutasi Siklis dan Contoh Soalnya
  
  

  
  Posting kali ini akan membahas tentang Permutasi Siklis atau dengan kata lain Susunan Melingkar dikarenakan permutasi ini dilakukan dengan membuat susunan yang dipadu secara melingkar. Sebelumnya sudah kami terbitkan posting tentang  Permutasi dan Kombinasi. Bedanya, posting kali ini membahas tentang bagian dari Permutasi yaitu Permutasi Siklis.
  
  

  
  

  
  

  PERMUTASI SIKLIS ( SUSUNAN MELINGKAR )
  Permutasi siklis berkaitan dengan penyusunan sederetan objek yang melingkar. Sebagai contoh adalah susunan duduk dari beberapa orang pada meja bundar. Permutasi ini juga dikenal dengan permutasi melingkar.
  
  A. RUMUS

  
  
  
  

  Bagaimana menentukan rumus permutasi siklik ?
  Perhatikan contoh berikut :
  Tentukan susunan yang dapat terjadi jika :
  o Ada 2 orang A1, A2 didudukkan dalam meja bundar ?
  o Ada 3 orang A1, A2, A3 didudukkan dalam meja bundar ?
  o Ada 4 orang A1, A2, A3, A4 didudukkan dalam meja bundar ?
  o Ada n orang A1, A2, A3, . . . . .,An didudukkan dalam meja bundar ?
  Jawab :
  Susunan pengaturan duduk pada 2 orang ada 1 yaitu
  o A1, A2
  Susunan pengaturan duduk pada 3 orang ada 2 yaitu
  o A1, A2, A3 dan
  o A1, A3, A2
  Susunan pengaturan duduk pada 4 orang ada 6 yaitu
  o A1, A2 , A3 , A4
  o A1, A2 , A4 , A3
  
  o A1, A3 , A2 , A4
  o A1, A3 , A4 , A2
  o A1, A4 , A2 , A3
  o A1, A4 , A3 , A2
  Tampak di sini bahwa A1 sebagai patokan diletakkan di urutan paling depan, sedangkan urutan selanjutnya adalah permutasi dari (A2 , A3 , A4) = 3! =6
  
  Susunan pengaturan duduk pada n orang yaitu....?

  
  
  

  
  Dengan penalaran yang sama dengan diatas maka A1 dinyatakan sebagai patokan yang ditulis pada urutan terdepan, sedangkan urutan berikutnya(A2 , A3 , A4 ,……,An) yang memiliki (n-1) anggota sehingga jika dipermutasikan terdapat (n-1) ! macam permutasi yang berbeda
  
  Dengan demikian banyak permutasi siklik yang beranggotakan n adalah (n-1) !

  
  

  Jika masih belum paham, berikut kami sajikan Contoh Soalnya:

  
  

  
  

  
  

  Contoh Soal:

  
  

  Sebanyak 6 orang anggota DPR, mengadakan rapat. Mereka duduk menghadap sebuah meja bundar (seperti Konferensi Meja Bundar saja, hehehhe) Berapa banyak cara mereka dapat menempati kursi yang disusun melingkar tersebut.

  
  

  
  

  
  

  Jawab:

  
  

  Soal ini tergolong mudah, kita tinggal memasukkannya pada rumus umum Permutasi Siklis di atas. Dengan nilai n = 6.

  
  

  
  

  
  

  Psiklis = (n-1)!

  
  

  Psiklis = (6 - 1)!

  
  

             = 5 !

  
  

             = 120 cara

  
  

  Jadi, terdapat sebanyak 120 cara membagi temapat duduk untuk keenam orang tersebut..

  Bagaimana, mudah bukan. Semoga bermanfaat bagi teman-teman.
  
  
  
  
  
  
   

  Bab 12

  Modus Ponens, Modus Tollens dan Contohnya

  
  

  
  
  

  Pembelajaran tentang modus ponens, modus tollens kali ini akan kita dapat di kleas X SMA, kalau tidak salah judul babnya adalah Logoika Matematika. Terdapat 3 penarikan kesimpulan yang sah untuk tiap persoalan logika matematika yaitu sebagai berikut:

  model 1:
  Diketahui premis-premis berikut.
  premis (1) : p —> q
  premis (2) : p
  kesimpulan : q
  pola penarikan kesimpulan argumentasi di atas adalah modus ponens.

  Arti Modus Ponens adalah “jika diketahui p → q dan p, maka bisa ditarik kesimpulan q“.

  model 2:
  Diketahui premis-premis berikut.
  premis (1) : p —> q
  premis (2) : -q
  kesimpulan : -p
  pola penarikan kesimpulan argumentasi di atas adalah modus tolens.

  Sedangkan Modus Tollens berarti “jika diketahu p → q dan ¬q, maka bisa ditarik kesimpulan ¬p“.

  model 3:
  Diketahui premis-premis berikut.
  premis (1) : p —> q
  premis (2) : q —> r
  kesimpulan : p —> r
  pola penarikan kesimpulan argumentasi di atas adalah silogisme.

  Berikut adalah contoh soal yang masuk dalam Ujian Nasioanl tahun 2006/2007:

  Diketahui pernyataan:

  1. Jika hari panas, maka Ani memakai topi

  2. Ani tidak memakai topi atau ia memakai payung

  3. Ani tidak memakai payung

  Kesimpulan yang sah adalah 

  a. hari panas

  b. hari tidak panas 

  c. Ani memakai topi

  d. hari panas dan Ani memakai topi

  e. hari tidak panas dan ani memakai topi

  Penyelesaian untuk kasus tersebut adalah seb agai berikut:

  p = hari panas

  q = Ani memakai topi

  r = Ani pakai paying

  
  

  p        q

  ~q ᶸ r

  ~r

  ~p

  Untuk pembuktian dengan percobaan Benar dan Salah, kasus ini terbukti tautology. Sehingga jawaban yang mungkian adalah B. hari tidak panas ( ~p)

  Semoga materi tentang modus ponens, modus tollens kali ini dapat membantu, jangan lupa untuk membaca materi matematika lainnya.

    Bab 13

  Rumus Luas dan Keliling Persegi, Segitiga dan Lingkaran 

  
  
  

  
  

  
  
  

  Rumus Luas dan Keliling Persegi, Segitiga dan Lingkaran - Kali ini postingannya mengenai matematika lagi nih sobat, Yaitu bagian dari rumus-rumus beberapa bangun datar, seperti Persegi, Persegi Panjang dan Segitiga. Ada juga postingan terdahulu mengenai Luas dan Volume bangun Kerucut.

  
  

  
  Rumus Persegi
  Keliling : 4 x Sisi
  contoh : Sisi = 5  cm² 
  Keliling = 4 x 5
  = 20 cm
  
  Luas : Sisi x Sisi

  
  

  
  Contoh Soal: 

  
  

  Diketahui sisi = 5 cm
  Maka luas = 5 x 5
                 = 25 cm²
   
  

  
  

  Rumus persegi panjang

  
  

  Keliling : 2 x (Panjang + Lebar)

  
  

  
  

  
  

  Contoh soal: 

  
  

  Diketahui panjang = 6 cm
  Lebar = 4 cm
  Keliling = 2 x (6 + 4)
  = 20 cm
  
  Luas : Panjang x Lebar
  Contoh soal: 

  
  

  Diketahuui panjang = 7 cm
  lebar = 4 cm
  Luas = 7 x 4
  = 28 cm²
  Rumus SegitigaKeliling : AB + AC + BC

  
  

  
  Contoh soal: 

  
  

  AB = 7 cm
  AC = 10 cm
  BC = 5 cm

  
  

  
  Kelililng : 7 + 10 + 5
  = 22 cm
  
  Luas Segitiga : 1/2 x alas (BC) x tinggi AB
  1/2 x 6 x 8
  = 24 cm²
  Rumus Lingkaran

  
  

  Keliling lingkaran :22/7 x diameter atau 2 x 22/7 x jari jari
  
  contoh soal: 

  diameter =28 cm
  jari jari = 2 x diameter = 28 : 2 = 14 cm
  Keliling : 22/7 x 28 = 88 cm
  
  Luas lingkaran : (22/7 atau 3,14) x jari jari (r)
  = 22/7 x 14 x 14
  = 44 x14
  = 616 cm2
  
  
  
  

  ☺☺ Selamat Belajar ☺ ☺